反轉變換及相切圓
Inversion and Tangent Circles
數學算板(MathBoard)程式提供了許多變換(Transformation)的功能,除平移(Translation)、旋轉(Rotation)、鏡射(Reflection)、相似(Dilation)、基軸(Basic Coordinate Transformation)等變換之外,另外提供了反轉變換(Inversive transfromation)、極軸變換(Polar-Pole Transformation)的功能。
設O(r) 表示平面上圓心為O,半徑為r的圓,設P為平面上異於O的任意一點,在OP射線上一點P',若滿足 OP × OP' = r2,則稱P' 為P對圓O之反轉點(像image),圓O(r)稱為反轉圓 (circle of inversion),O點稱為反轉中心(center of inversion),r 稱為反轉半徑(radius of inversion)。若P點與O點重合,P點之反轉點定義為無窮遠點 (point at infinity)。加上此無窮遠點的平面,稱為反轉平面(Inversive plane)。反轉平面上這種點對應的方式,稱為反轉變換 (Inversive transformation)。幾何圖形反轉後,可得到反轉圖形。經過反轉點P'作垂直於OP之直線,稱為軸 (polar),P點稱為極點(pole),這個點與直線的變換稱為極軸變換(Reciprocation或Polar-Pole Transformation)。
MathBoard 反轉點作圖步驟:
(1) 以O為圓心,r為半徑,作圓。
(2) 在平面上任取一點P,作射線OP,交圓O於於A點。
(3) 以O為放縮中心, OA/OP為放縮比率,將A點放縮,得點P' 即為所求。
由於反轉變換保持相切的性質,透過適當的反轉圓選取,反轉變換可將相切或相離的兩個圓變換為兩平行線或同心圓,在平行線或同心圓間,作出與平行線或同心圓相切且彼此相切的圓,再將這些圓反轉變換回去,就可以得到與原來兩圓相切且彼此相切的圓。本頁對相關相切圓及反轉變換做一簡單介紹。
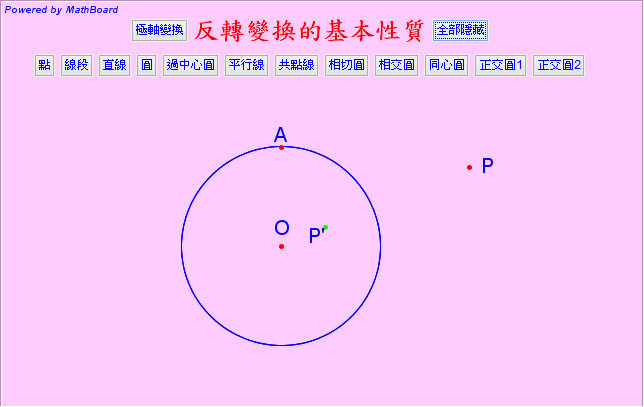
一、反轉變換的基本性質
在數學算板(MathBoard)中,標定反轉圓後,可以對選取的點、線段、射線、直線、圓等物件做反轉變換,點的反轉像為點,線段的反轉像為弧,射線的反轉像為一個端點在反轉圓心的弧,直線的反轉像為直線本身(若原直線通過反轉圓心)或過反轉圓心的圓(原直線不通過反轉圓心),圓的反轉像為直線(原圓通過反轉圓心)或圓(原圓不通過反轉圓心)。本程式(如下圖)提供了相關的按鈕,可供使用者呈現物件的反轉結果,除了上述基本結果之外,也提供了平行線、相切圓、正交圓、…等的轉換結果。
下列輪換按鈕會呈現或隱藏,所述的物件及其反轉像,並展示其性質,使用者可以用滑鼠移動該物件,觀察像的相應變化。
點、線段、射線、直線、圓、過中心圓、共點線:均呈現該物件及其反轉像。此外,
平行線:呈現兩條平行線,及其反轉像(過反轉中心的相切圓)。因此,在此平行線間作出與平行線相切且彼此相切的圓(容易),反轉之後,就可得到與相切兩圓相切且彼此相切的圓。
相切圓:呈現兩相切圓,及其反轉像,注意當圓通過反轉圓心時,像的變化。
相交圓:呈現兩相交圓,及其反轉像,並呈現兩圓心與交點構成的角,其度數不變。
同心圓:呈現兩同心圓,及其反轉像(兩相離的圓)。因此,在此同心圓間作出與同心圓相切且彼此相切的圓(容易),反轉之後,就可得到與相離兩圓相切且彼此相切的圓。
正交圓1:呈現與反轉圓正交的圓,此圓的反轉像就是本身。
正交圓2:呈現任意兩正交圓,及其反轉的兩正交圓。
極軸變換(Polar-Pole Transformation):基於反轉的點對線的變換。
二、反轉觀點的圓錐曲線
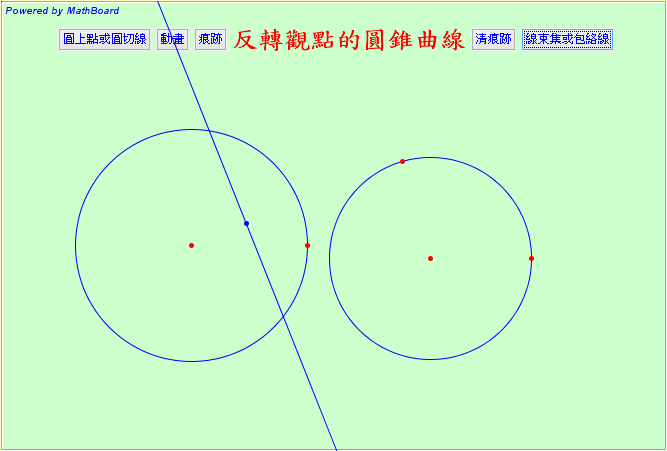
本程式呈現圓反轉(the reciprocal of a circle)觀點的圓錐曲線(如下圖)。
設C表示一個圓上所有的點所成集合,C就是圓上一點的軌跡(Locus),T表示此圓所有的切線所成集合,此時,C就是T的包絡線(Envelope),將這個兩個集合(點集合C及切線集合T)對另一圓O作極軸變換(reciprocation),點集合C變換為直線集合C',切線集合T變換為點集合T',這個線集合C'的包絡曲線就是點集合T',而T'恰為圓錐曲線。
本程式中有列按鈕:
(1)圓上點或圓切線 ─ 本按鈕輪換呈現圓上點模式及圓切線模式,前者呈現圓上點經極軸變換而得的直線,後者呈現圓切線經極軸變換而得的點。
(2)動畫 ─ 本按鈕會動態模擬切點及切線,其極軸變換而得的結果也會做動態變換。
(3)痕跡 ─ 本按鈕秀藏極軸變換結果在動畫狀態時,呈現的痕跡(線束或點軌跡)。
(4)清痕跡 ─ 本按鈕清除前述痕跡。
(5)線束集或包絡線 ─ 本按鈕呈現或隱藏,所有圓上點經極軸變換而得的線束集物件(圓上點模式),或所有切線經極軸變換而得的點集合軌跡曲線(圓切線模式),前者的包絡線就是就是後者,它們是圓錐曲線。線束或包絡線為物件,其形狀會隨反轉圓及原始圓的相對位置而改變,可能是雙曲線或拋物線或橢圓,或它們的切線集。
三、帕伯斯(Pappus)的古定理
帕伯斯的古定理 ( Pappus' Ancient Theorem )
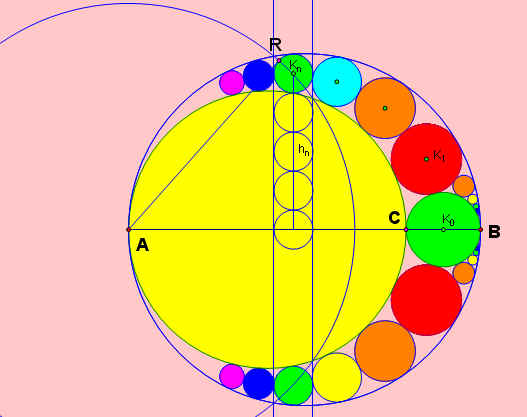
設A,B,C為共線三點,C介於A,B之間,作以AC、AC、BC為直徑的三個圓,設圓K0、K1、K2、…、Kn、…為依序相切圓的圓,這些圓均與以AB、AC為直徑的圓相切(如圖),設其半徑分別為r0、r1、r2、…rn、…。令Kn至AB直線的距離為hn,則
hn = 2nrn
本定理可透過反轉變換證得,作出圓的切線段AR,其中R為切點,以AR為半徑作圓,以圓A為反轉圓,將過A的兩個相切圓反轉可得與AB相垂直的兩條平行線,將圓K0、K1、K2、…、Kn作反轉可得與此二平行線相切的一串相切圓(n+1個),其中圓Kn反轉後就是自己(因為它與圓A正交),圓K0反轉為圓心在AB線段上的圓,故知 hn = 2nrn。
本程式製作的基本過程如下:(請按反轉原理觀察)
(1)作出AB直線,並在其上取C點,作出分別以AB,AC,BC為直徑的三個相切圓
(2)以A為圓心,AB為半徑,作圓。
(3)以圓A為反轉圓,對前述三圓作反轉變換,過A點的相切圓反轉為兩平行線,以CB直徑的圓反轉後為與此二平行線相切的圓(參閱反轉變換的幾本性質)
(4)在此二平行線間作出相切的其他的圓
(5)將平行線間的圓再以圓A作反轉變換,可得三個原始相切圓間的相切圓(AB下方的圓,可透過AB鏡射獲得)
(6)其他組圓,可以由類似的方法製作出來。
四、史丹納圓鏈(Steiner's Chain)
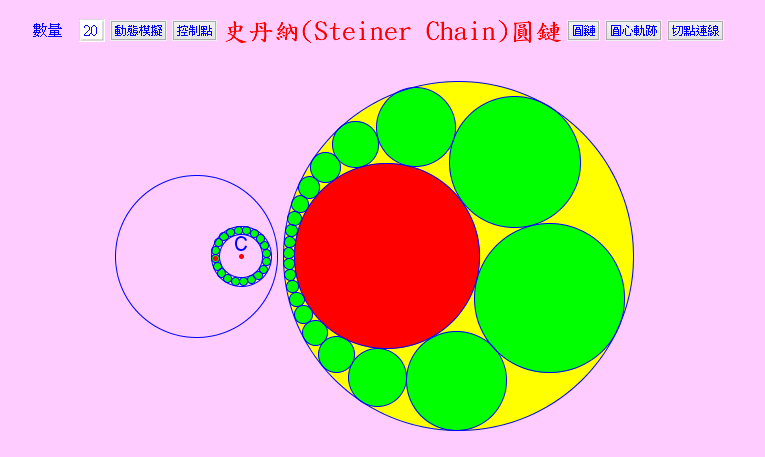
本程式展示史丹納圓鏈。設有二圓內離,若此二圓之間能依序插入一串與此二圓相切但又與前一相鄰圓相切的圓,且最後一個圓與第一個圓相切,這一串圓稱為史丹納圓鏈(Steiner's Chain)如下圖。
程式並提供輸出入框及按鈕:
(1)數量:雙擊輸出入框後輸入數字並按Enter,該數表示圓鏈中圓的的個數,最多20個。
(2)動態模擬:按鈕可另圓鏈轉動,再按則停止。
(3)控制點:展示或隱藏控制點,可控制相關圓的大小及位置。
(4)圓鏈:整理圓鏈,使圓鏈中各圓相切(剛輸入圓鏈數量時,圓鏈中圓可能並未相切)。
(5)圓心軌跡:展示或隱藏圓鏈的圓心軌跡 ─ 橢圓。
(6)切點連線:圓鏈上任一圓與兩內離圓切點線 ─ 它們都通過一個定點。
本程式圖形基本製作過程是:作出兩個同心圓CA及CB,在兩個同心圓間插入相切圓,然後以圓OR為反轉圓,將所有的圓作反轉變換(Inversive Transformation)即得,同心圓作反轉變換得兩內離圓(反之亦然)。設兩同心圓半徑分別為 a , b ,且 a > b,若
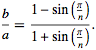
則同心圓內恰好可以插入n個相切圓。
圓鏈的圓心軌跡為一個橢圓(Ogilvy 1990, p. 57),當內離圓為同心圓時,圓鏈圓心軌跡為一個橢圓。又圓鏈上任一圓與兩內離圓相切之切點的連線均會通過一定點。
參考書目
Coxeter, H. S. M. and Greitzer, S. L. Geometry Revisited. Washington, DC: Math. Assoc. Amer., pp. 124-126, 1967.
Ogilvy, C. S. Excursions in Geometry. New York: Dover, pp. 51-54, 1990.
五、兩圓公切圓的圓心軌跡
本程式呈現兩圓公切圓的圓心軌跡。學生可先探討如何以幾何作圖法做出兩圓公切圓,之後可透過本程式之操作,探討不同的兩圓關係之下,其公切圓圓心的軌跡是什麼,有幾組公切圓。也可以研究,當兩圓退化為一點,或一直線時,其公切圓圓心軌跡圖形又是什麼形狀。
製作一般的兩圓及其公切圓,原理並不難,透過GSP的一般化功能,只要做出兩圓相離時的兩個公切圓,利用軌跡功能,即可十分容易的得到兩圓公切線的圓心軌跡,透過兩圓關係(外離、相交、內離)及半徑的改變,就可看到多種變化的情形。公切圓之作圖步驟列出如下:
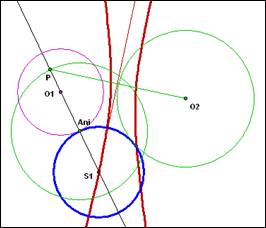
(1) 分別做出兩外離圓,圓O1及圓O2。
(2) 在圓O1上取一動點Ani,做出連接O1的直線L。
(3) 以為圓心,圓O2之半徑為半徑作圓,交L直線於P,Q兩點。
(4) 作PO2線段的垂直平分線,交直線L於S1點,以S1為圓心,過Ani作圓,此圓即為圓O1及圓O2的外公切圓。
(5) 作QO2線段的垂直平分線,交直線L於S2點,以S2為圓心,過Ani作圓,此圓即為圓O1及圓O2的內公切圓。
(6) 分別做出S1及S2的軌跡,即為公切圓圓心軌跡。
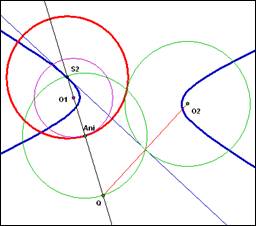
教師可適度分析作圖的思考方向,亦即引導學生假設圖形已作出來,再作逆推的思考。若要證明軌跡必為雙曲線(或在其他兩圓關係下,為其他圓錐曲線),由垂直平分線之作圖過程,很容易就可看出S1O1與S1O2 兩線段的差(或和)為兩圓半徑的差(或和),或S2O1與S2O2 兩 線段的差(或和)為兩圓半徑的差(或和),參看下二圖。
有關這個主題的相關討論,請參閱
林保平 (民93). 公切圓之圓心軌跡─用動態幾何軟體探討幾何性質。科學教育月刊,第271期,pp2-9。
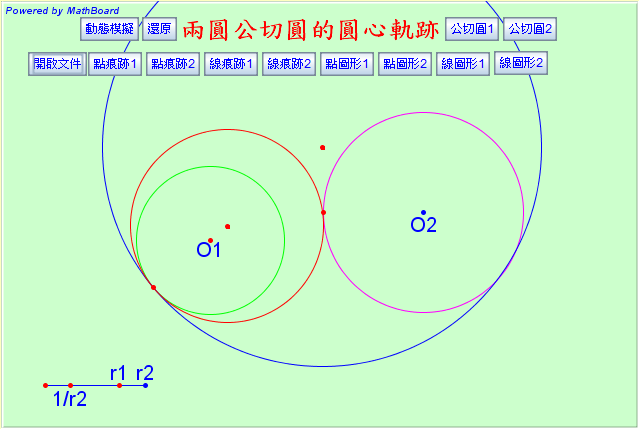
下圖為本展示程式的畫面:
本程式按鈕功能說明如下:
(1)動態模擬:展示切點在圓O1上移動時,兩公切圓所在的位置。
(2) 還原:r1、r2位置表示圓O1、O2的半徑長。可移動點r1及點1/r2來改變圓半徑,當r1趨近0時,圓O1趨近一個點,當1/r2趨近0時,圓O2趨近一條直線,「還原」按鈕可還原半徑至啟始位置。
(3)公切圓1、公切圓2:展示或清除公切圓。
(4)點痕跡1、點痕跡2:當動態模擬時,展示兩公切圓圓心的路徑的點痕跡。
(5)線痕跡1 、線痕跡2:當動態模擬時,展示前述垂直平分線移動的痕跡。
(6)點圖形1、點圖形2:展示兩公切圓圓心的路徑的圖形,這是兩條圓錐曲線。
(7)線圖形1 、線圖形2:展示前述垂直平分線移動的的路徑線束。
(8)開啟文件:打開本程式的說明文件。(其內容與本說明相同)
六、三點為圓心兩兩相切的圓
本程式展示三點為圓心兩兩相切的圓,其基本作圖方法為:
設三角形ABC三邊長分別為a,b,c,利用連心線、內外切、半徑之關係,解聯立方程式,可分別求出圓A的半徑與AB(亦即c)的比值(a+b+c)/2c,(b+c-a)/2c 及 (a+b-c)/2c。分別找出這三個位置的點,再作出三圓即可。
七、三個兩兩相切圓的公切圓
本程式圖形,實為帕伯斯古定理圖形的一部份。
 ,/
,/